
트리(Tree)란?
트리 구조란 노드들이 나무 가지처럼 연결된 비선형 계층적 자료구조이다.
용어

트리 구조를 보며 알아야 할 용어들이 몇 개 있다.
부모 노드(parent node) : 자기 자신(노드)과 연결된 노드 중 자신보다 높은 노드를 의미 (ex. F의 부모노드 : B)
자식 노드(child node) : 자기 자신(노드)과 연결 된 노드 중 자신보다 낮은 노드를 의미 (ex. C의 자식노드 : G, H)
루트 노드 (root node) : 일명 뿌리 노드라고 하며 루트 노드는 하나의 트리에선 하나밖에 존재하지 않고, 부모노드가 없다. 위 이미지에선 녹색이 뿌리노드다.
단말 노드(leaf node) : 리프 노드라고도 불리며 자식 노드가 없는 노드를 의미한다. 위 이미지에서 주황색 노드가 단말노드다.
내부 노드(internal node) : 단말 노드가 아닌 노드
형제 노드(sibling node) : 부모가 같은 노드를 말한다. (ex. D, E, F는 모두 부모노드가 B이므로 D, E, F는 형제노드다.)
깊이(depth) : 특정 노드에 도달하기 위해 거쳐가야 하는 '간선의 개수'를 의미 (ex. F의 깊이 : A→B→F 이므로 깊이는 2가 됨)
레벨(level) : 특정 깊이에 있는 노드들의 집합을 말하며, 구현하는 사람에 따라 0 또는 1부터 시작한다. (ex. Level 3 - D, E, F, G, H)
차수(degree) : 자식 노드 개수 (ex. B의 차수 = 3 {D, E, F} )
높이(height): 깊이 중 최댓값 (트리의 높이: 3)
특징
- 일반적으로 대상정보의 각 항목들을 계층적으로 구조화할 때 사용하는 비선형 자료구조
- 데이터의 '저장'의 의미 보다는 저장된 데이터를 더 효과적으로 '탐색' 하기 위해서 사용된다.
- 리스트와 다르게 데이터가 단순히 나열되는 구조가 아니라, 부모(parent)와 자식(child)의 계층적인 관계로 표현된다.
- 트리는 그래프(Graph)의 한 종류이며, 사이클이 없다.
- 트리에서 Root Node를 제외한 모든 노드는 단 하나의 부모노드를 가진다.
- 트리는 이진 트리, 이진 탐색 트리, 균형 트리(AVL 트리, red-black 트리), 이진 힙(최대힙, 최소힙) 등이 있다.
순회
전위 순회 (Preorder)
깊이 우선 순회라고도 불린다.
루트 노드 -> 왼쪽 서브 트리 -> 오른쪽 서브 트리 (VLR)
루트 노드(Visited) - 방문
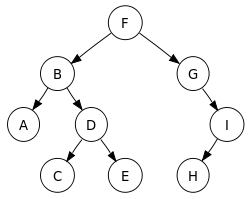
1. 루트 노드 F 방문
2. F의 왼쪽 서브 트리의 루트 노드 B 방문
3. B의 왼쪽 서브 트리의 루트 노드 A 방문
4. B의 오른쪽 서브 트리의 루트 노드 D 방문
5. D의 왼쪽 서브 트리의 루트 노드 C 방문
6. D의 오른쪽 서브 트리의 루트 노드 E 방문
7. F의 오른쪽 서브 트리의 루트 노드 G 방문
8. G의 오른쪽 서브 트리의 루트 노드 I 방문
9. I의 왼쪽 서브 트리의 루트 노드 H 방문
탐색 순서
F B A D C E G I H
중위 순회 (Inorder)
왼쪽 서브 트리 -> 루트 노드 -> 오른쪽 서브 트리 (LVR)

<F의 왼쪽 서브 트리>
1. 루트 노드 B의 왼쪽 서브 트리의 루트 노드 A 방문
2. 루트 노드 B 방문
<B의 오른쪽 서브트리>
3. 루트 노드 D의 왼쪽 서브 트리의 루트 노드 C 방문
4. 루트 노드 D 방문
5. 루트 노드 D의 오른쪽 서브트리의 루트 노드 E 방문
<루트 노드 F>
6. 루트 노드 F 방문
<F의 오른쪽 서브트리>
7. 루트 노드 G 방문
<G의 오른쪽 서브트리>
8. 루트 노드 I의 왼쪽 서브 트리의루트 노드 H 방문
9. 루트 노드 I 방문
탐색 순서
A B C D E F G H I
후위 순회(Postorder)
왼쪽 서브 트리 -> 오른쪽 서브 트리 -> 루트 노드 (LRV)

< F의 왼쪽 서브 트리>
1. 루트 노드 B의 왼쪽 서브 트리 A 방문
<B의 오른쪽 서브 트리>
2. D의 왼쪽 서브 트리의 루트 노드 C 방문
3. D의 오른쪽 서브 트리의 루트 노드 E 방문
4. 루트 노드 D 방문
<B의 루트 노드>
5. 루트 노드 B 방문
<F의 오른쪽 서브 트리>
<G의 오른쪽 서브 트리>
6. 루트 노드 I의 왼쪽 서브 트리의 루트 노드 H 방문
7. 루트 노드 I 방문
<G의 루트 노드>
8. 루트 노드 G 방문
<F의 루트 노드>
9. 루트 노드 F 방문
탐색 순서
A C E D B H I G F
Reference
https://code-lab1.tistory.com/9
https://velog.io/@kimdukbae/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%ED%8A%B8%EB%A6%AC-Tree
'☁️ Algorithm' 카테고리의 다른 글
| 약수 알고리즘 (Java) (0) | 2023.05.17 |
|---|---|
| 이진 탐색 트리(Binary Search Tree) (Java) (0) | 2023.05.03 |
| 이진 탐색(Binary Search) (Java) (0) | 2023.05.03 |
| [알고리즘] 조합(Combination) (Java) (0) | 2023.03.21 |
| [알고리즘] BFS (Java) (0) | 2023.03.15 |




댓글